Переменный ток
Переменный синусоидальный ток (а так же и переменное напряжение) изменяется со временем по амплитуде (величине) и направлению движения электронов. На графике переменный ток имеет вид синусоиды. Переменный ток может иметь различную форму, но в промышленности, в быту и радиоэлектронных приборах наибольшее распространение получил именно синусоидальный ток.

Конденсатор в цепи переменного тока
Для исследования свойств конденсатора соберём схему, показанную на рисунке. Для измерений нам потребуются два прибора - функциональный генератор и мультиметр.
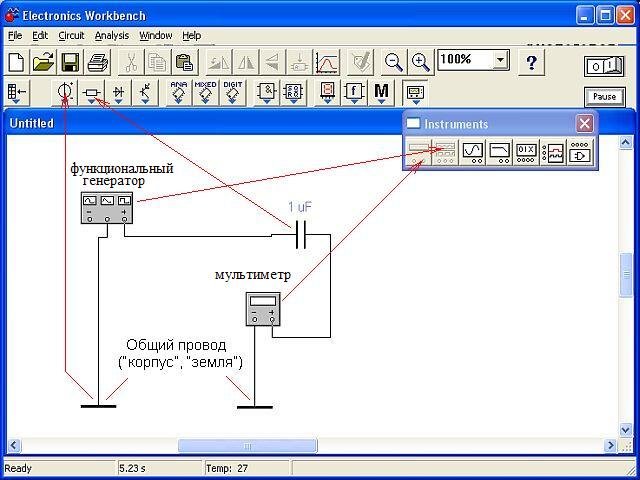
(Стрелками указаны панели инструментов, на которых расположены элементы).
Для проведения экспериментов настроим генератор на определённые параметры. Для этого, двойным щелчком мыши следует развернуть панель настройки генератора и внести изменения, показанные на рисунке:

Аналогичным образом следует развернуть панель мультиметра, и включить определённые переключатели.
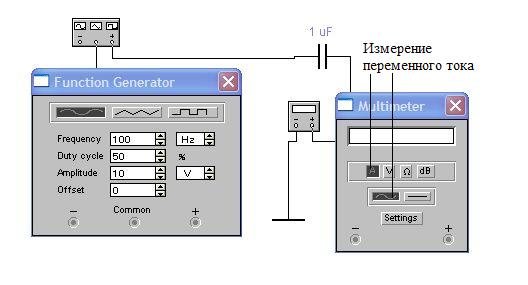
Ёмкость конденсатора оставим без изменения, равной 1 микрофараде (1mF).
Для постоянного тока сопротивление конденсатора можно считать бесконечно большим, так как оно равно сопротивлению диэлектрика помещённого между обкладок конденсатора. Иначе дело обстоит при включении конденсатора в цепь переменного тока (далее, под переменным током будет подразумеваться синусоидальный ток). Так как переменный ток со временем меняет своё направление и амплитуду, то конденсатор в цепи заряжается и разряжается, то есть в цепи возникает электрический ток. Включим нашу схему и убедимся, что через конденсатор проходит электрический ток.
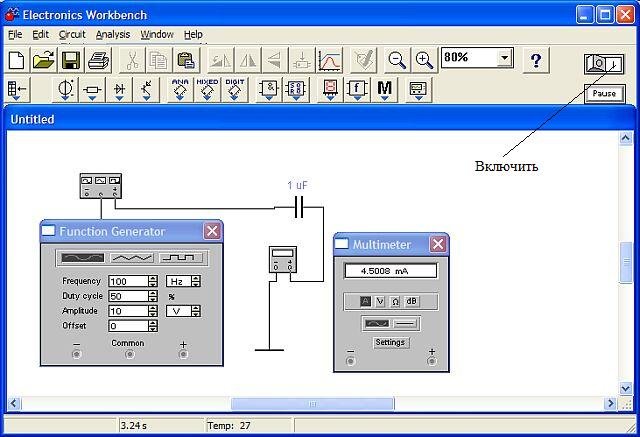
Мы видим, что амперметр показывает ток, проходящий через конденсатор, равный 4,5 миллиампера. Попробуем увеличить частоту генератора до 1000 Гц (1кГц).

Мы видим, что ток вырос до 45 мА, хотя напряжение источника переменного тока мы не меняли. Попробуем изменить значение ёмкости конденсатора, увеличив её до 10 мКф. Ток через конденсатор опять увеличился и составил 450 мА.
Из поставленного эксперимента следует, что сопротивление конденсатора переменному току зависит от частоты переменного тока и ёмкости конденсатора.
Сопротивление конденсатора переменному току (Xc) вычисляется по формуле:
Xc = 1/(2*pi*f*C)
где: pi = 3,14, f - частота в Герцах (Гц, Hz), c - ёмкость в Фарадах (F).
Для расчёта параметров конденсаторов и катушек индуктивности вы можете воспользоваться специальным калькулятором на сайте
Рассчитаем ёмкостное сопротивление конденсатора для нашего первого случая, где С = 1mF и частота f = 100 * 10-6 F;
Xc = 1/(2*3,14*100*10-6) = 1592,35668789809 = 1592,4 Oм.
Установленная в генераторе амплитуда переменного напряжения 10 V является амплитудным напряжением - Uа. Измерительные приборы показывают действующее (эффективное) значение переменного напряжения, которое вычисляется по формуле Uэф = Uа * 0,707, то есть, в нашем случае, Uэф = 10 * 0,707 = 7,07 V. Вольтметр, подключенный к генератору, показывает именно эффективное значение:

Тогда ток, проходящий через конденсатор, (по закону Ома I=U/R) будет: I = Uэф/Xc = 7,07/1592,4 = 0,0044 А = 4,4 мА, что совпадает с измеренным результатом.

Параллельное и последовательное включение конденсаторов.
При параллельном включении конденсаторов, общая ёмкость равна сумме ёмкостей всех включенных параллельно конденсаторов.
Co = C1 + C2 + ... + Cn
Из этого следует, что общий переменный ток, проходящий через конденсаторы равен сумме токов проходящих через каждый конденсатор.
Убедимся на примере, что это именно так. Вернёмся к предыдущему примеру, установив частоту генератора 1000 Гц и ёмкость конденсатора 1 мкФ.

В такой цепи ток, проходящий через конденсатор равен 45 мА. Подключим параллельно ещё один конденсатор, также ёмкостью 1 мкФ.

Мы видим, что суммарная ёмкость увеличилась в два раза, соответственно и переменный ток возрос в два раза.
Иначе обстоит дело при последовательном включении конденсаторов. Здесь общая ёмкость рассчитывается по формуле:
1/Co = 1/C1 + 1/C2 + ... + 1/Cn
Результирующая ёмкость не может быть больше наименьшей ёмкости составляющих цепочку конденсаторов.
Вернёмся к нашей схеме и включим два конденсатора последовательно.
Рассчитаем общую ёмкость цепи: 1/Co = 1/1 + 1/1 = 2; Co = 1/2 = 0,5

При такой ёмкости, ток в цепи будет 22,5 мА.

Катушка индуктивности в цепи переменного тока
С катушкой индуктивности ситуация прямо противоположная конденсатору. Катушка индуктивности обладает ничтожным сопротивлением постоянному току, так как зависит от числа витков и площади сечения проводника обмотки. В цепи переменного тока катушка обладает реактивным сопротивлением, которое вычисляется по формуле:
XL = 2 * 3,14 * f * L
Где f - в Герцах и L - в Генри.
Соберём схему, показанную на рисунке (катушка находится на той же инструментальной панели, что и конденсатор):
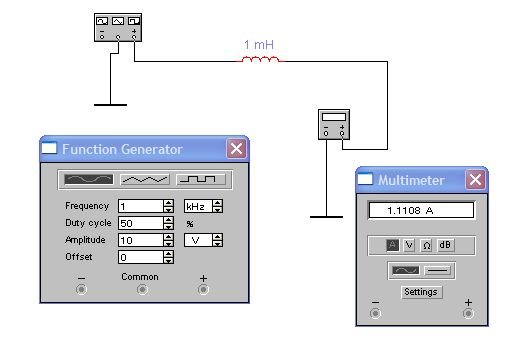
Рассчитаем ток, проходящий через катушку, и сравним с измеренным значением.
Сопротивление: XL = 2 * 3,14 * 1000 * 1*10-3 = 6,28 Ом;
Ток: I = Uэф/XL = 7,0721/6,28 = 1,126130573248 - что близко к измеренному значению.
Попробуем ступенчато увеличивать частоту генератора и отслеживать изменение тока в цепи. Результаты измерений удобно заносить в электронную таблицу Excel или OpenOffice Calc.

Проведя измерения согласно данных таблицы, построим график зависимости тока через катушку от частоты
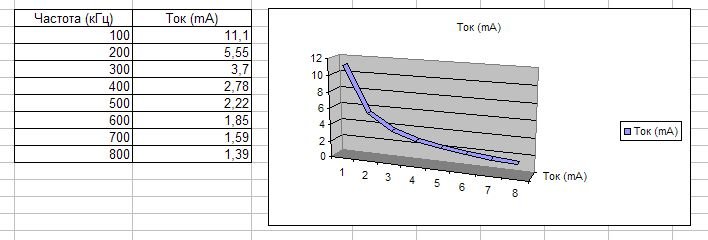
По результатам измерений и на графике мы видим, что ток через катушку уменьшается с увеличением частоты, причём эта зависимость нелинейная.

Параллельное и последовательное включение катушек индуктивности
При последовательном соединении катушек индуктивности суммарная индуктивность равна сумме индуктивностей последовательно включенных катушек:
Lo = L1 + L2 + ...+Ln
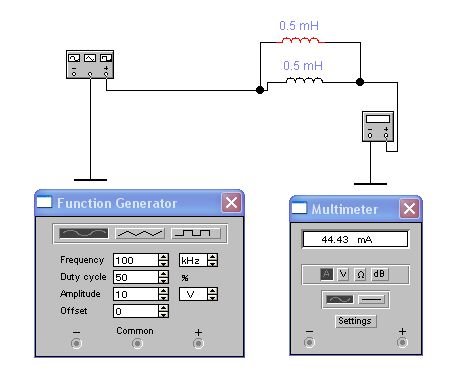
Чтобы не производить дополнительных расчетов, из предыдущей схемы составим новую, добавив ещё одну катушку, включив её последовательно, и заменим значения индуктивности обеих катушек на 0,5 мГн.

Мы видим, что сумма индуктивностей равна 1 мГн и ток равен 11,11 мА, что соответствует измеренному значению в предыдущем эксперименте.
При параллельном соединении катушек индуктивности, их результирующая индуктивность вычисляется по формуле:
1/Co = 1/C1 + 1/C2 +...+ 1/Cn
Изменим схему включения катушек:
Рассчитаем суммарную индуктивность наших катушек:
1/Со = 1/0,5 + 1/0,5 = 4; Со = 1/4 = 0,25
Найдём индуктивное сопротивление:
ХL= 2 * 3,14 * 100000 * 0,25*10-3 = 157
Найдём ток, проходящий через катушки:
I = Uэф/XL = 7,0721/157 = 0.04504522293 А = 45,04 мА
Расчётный результат близок к измеренному значению.

Параллельный колебательный контур
Для исследования свойств параллельного колебательного контура следует собрать схему, показанную на рисунке:
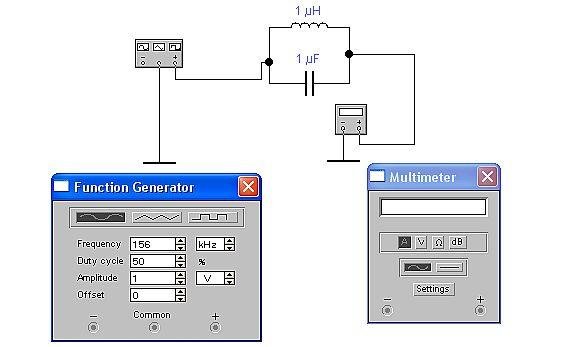
По умолчанию, ёмкость конденсатора равна 1 микрофараде и индуктивность катушки равна 1 миллигенри. На схеме следует заменить значение индуктивности на 1 микрогенри. Амплитуду выходного сигнала генератора следует установить равной 1 вольт, а диапазон частот в килогерцы (kHz).
По определению, резонансная частота колебательного контура, является такой частотой, при которой сопротивление контура принимает максимальное значение, то есть ток в цепи стремиться к нулю.
Резонансная частота (fp) колебательного контура рассчитывается по формуле:
fp = 1 / (2 * pi * (L * C)0,5) где pi = 3,14; L - в Генри; С - в Фарадах. Рассчитаем резонансную частоту нашего контура:
fр = 1 / (2 * 3,14 * (1*10-6 * 1*10-6)0,5 ) = 159235.668789809 Гц = 159,236 кГц.
Из расчета следует, что минимальный ток будет на частоте примерно 159 килогерц.
Построим резонансную кривую для колебательного контура, для обработки результатов измерений удобно воспользоваться электронной таблицей Microsoft Excel или Open Office Calc.

На рисунке А, показаны настройки генератора и амперметра. Изменяя частоту генератора по данным из электронной таблицы (Рис. Б) следует измерить ток и занести результаты измерения в таблицу.
Из полученных данных можно построить график резонансной кривой колебательного контура:

Мы видим, что резонанс наступает на частоте 157 кГц, что близко к расчётному значению. На резонансную частоту контура (в небольших пределах) влияют такие параметры, как паразитная ёмкость между витками катушки, температурная стабильность ёмкости и индуктивности, влияние нагрузки и тому подобное.
|
