Уравнения. Общие понятия
Уравнением с одним неизвестным х называется соотношение вида f(x)=0, где f(x) - какая-либо заданная функция действительного или комплексного переменного х.
Встречаются также уравнения вида f(x)=g(x), где f(x) и g(x) две заданные функции. f(x) - левая часть, g(x) - правая часть уравнения. Переносом g(x) в левую часть получаем f(x) - g(x)=0.
Уравнение следует рассматривать в области допустимых значений (ОДЗ), т.е. на множестве чисел х, на котором определены все входящие в уравнение функции. Для уравнения f(x) = 0 ОДЗ совпадает с областью определения функции f(x); для уравнения f(x) = g(x) ОДЗ есть пересечение областей определени левой и правой частей.
Решить уравнение - значит найти его корни(или решения), т.е. такие значения х, при подстановке которых в уравнение получается истинное равенство. Если корней в уравнении несколько их обычно нумеруют: x1,x2,x3 и так далее.
Два уравнения f1(x) = g1(x) и f2(x) = g2(x) называются равносильными (эквивалентными), если все корни первого уравнения являются корнями второго уравнения, а все корни второго уравнения - корнями первого.
Если все корни уравнения f1(x) = g1(x) удовлетворяют уравнению f2(x) = g2(x), то говорят, что уравнение f2(x) = g2(x) есть следствие уравнения f1(x) = g1(x).
Уравнения квадратные
Онлайн калькулятор
Квадратное уравнение: A * x2 + B * x + C = 0; Здесь A, B, C - коэффициенты (действительные или комплексные). Если А = 0, квадратное уравнение вырождается в линейное уравнение вида B * x+C=0.
Квадратное уравнение всегда имеет корни (действительные или комплексные), при действительных A, B, C вычисляемые следующим образом:
Вычисляем дискриминант D = B2 - 4 * A * C;
1) Если D = 0, корень один (двукратный): x = -(B / (2 * A));
2) Если D > 0, имеются два действительных корня:
x1 = (-B +
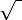D) / (2 * A),x2 = (-B -
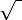D) / (2 * A).3) Если D < 0, нет действительных корней, а имеются два комплексных корня:
x1 = (-B + i *
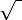D) / (2 * A),x2 = (-B - i *
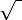D) / (2 * A). Где i - мнимая единица.При А <> 0 делением обеих частей на А квадратное уравнение приводится к виду x2 + p * x + q = 0 (приведённое квадратное уравнение).
Свойство корней приведённого квадратного уравнения x2 + p * x + q = 0 (теорема Виета):
x1 * x2 = q,
x1 + x2 = -p.
Уравнения с двумя неизвестными (система двух линейных уравнений)
Онлайн калькулятор
Система двух линейных уравнений с двумя неизвестными x и y имеет вид:
a1 * x + b1 * y = c1,
a2 * x + b2 * y = c2.
Уравнения составляющие систему имеют простой геометрический смысл: каждое уравнение задает некоторую прямую линию на плоскости xy. Решение системы - это координаты точки пересечения прямых. Очевидно, что если прямые параллелельны - решений нет, если прямые пересекаются в одной точке - решение единственно и если прямые совпадают то решений бесконечно много.
Для решения системы двух линейных уравнений составим определитель системы D:
D = a1 * b2 - a2 * b1.
Если D<>0, то решение существует и единственно, причем (по формулам Крамера):
x = Dx / D,
y = Dy / D
где:
Dx = c1 * b2 - c2 * b1,
Dy = a1 * c2 - a2 * c1.
Если D = 0, то решений нет, либо бесконечно много.
На практике удобно решать систему методом подстановки:
Одно из уравнений решаем относительно x или y (например y = (c1 - a1 *x) / b1) и подставляем это выражение в другое уравнение на место y; тогда получится линейное уравнение для одного неизвестного (в даннои случае для х).
Пример:
2 * x + 3 * y = 4
5 * x - 2 * y = 3
Из первого уравнения имеем x = 2 - 1,5 * y
подставляем х во второе уравнение и получаем:
5 * (2 - 1,5 *y) - 2 * y = 3 после преобразований получаем y = 14/19
Теперь х находится по формуле подстановки: x = 2 - 1,5 * 14 / 19 = 17/19