
 |
Онлайн калькуляторыПланиметрия |
|
Содержание: |
Площадь треугольника |
||
|
|
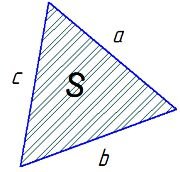 |
Площадь треугольника по 3 сторонам (формула Герона): S = sqrt(p*(p-a)*(p-b)*(p-c)); где sqrt - корень квадратный; p = (a + b + c)/2 - полупериметр. . (точка) Разделитель десятичный |
|
|
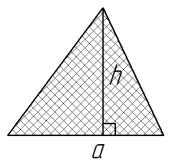 |
Площадь треугольника по основанию и высоте: S = a/2*h; где a - основание h - высота . (точка) Разделитель десятичный |
|
|
|
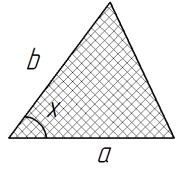
Площадь треугольника по 2 сторонам и углу: S = 1/2*a*b*sin(x) где x - угол (градусы); . (точка) Разделитель десятичный |

Площадь параллелограмма |
||
|
|
|
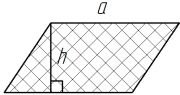
Площадь параллелограмма: S = a * h; где h - высота; а - основание . (точка) Разделитель десятичный |

Площадь трапеции |
||
|
|
|
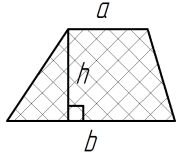
Площадь трапеции: S = (a +b)/2 * h; где h - высота; а и b - основания . (точка) Разделитель десятичный |

Площадь ромба |
||
|
|
|
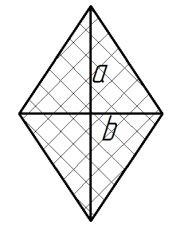
Ромб - параллелограмм с равными сторонами Площадь ромба: S = (a * b) / 2; где а и b - диагонали ромба . (точка) Разделитель десятичный |

Площадь круга |
||
|
|
|
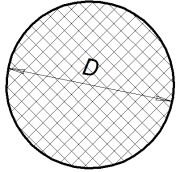
Площадь круга: S = (D/2)2*pi; где D - диаметр круга pi - константа 3.141593 . (точка) Разделитель десятичный |

Площадь кольца |
||
|
|
|
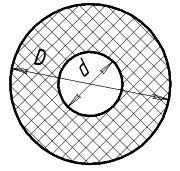
Площадь кольца: S = pi/4*(D2 - d2); где D - наружный диаметр кольца d - внутренний диаметр кольца pi - константа 3.141593 . (точка) Разделитель десятичный |

Площадь сектора круга |
||
|
|
|
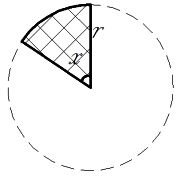
Площадь сектора круга: S = pi * r2 * x° / 360° где r - радиус сектора x - угол дуги сектора pi - константа 3.141593 . (точка) Разделитель десятичный |

Площадь сектора кольца |
||
|
|
|
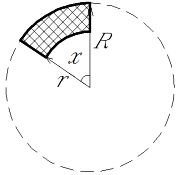
Площадь сектора кольца: S = pi * x° / 360 * (R2 - r2); где R - Наружный радиус кольца r - Внутренний радиус кольца x - угол дуги сектора pi - константа 3.141593 . (точка) Разделитель десятичный |

| ©НТТ Гуков К. М. 2006 - 2016 Почта: [email protected] |