Выбор элементов и сборка электрических схем в программе EWB.
Рассмотрим интерфейс программы EWB. Программа состоит из строки меню, ниже меню расположены панель системных кнопок (файлы, печать, масштаб и т.д.), панель инструментальных кнопок (выбор различных компонентов РЭА и измерительных приборов) и листа для рисования электронных схем.
Элементы электрических схем сгруппированы по категориям на панели инструментальных кнопок.
На рисунке показана панель Sources (Источники) на которой сгруппированы такие элементы как "заземление", источники постоянного и переменного тока и т.п.
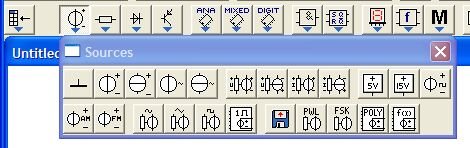
На панели Basic "Базовые элементы", сгруппированы такие элементы, как постоянные и переменные резисторы и конденсаторы, катушки индуктивности, трансформаторы и переключатели.
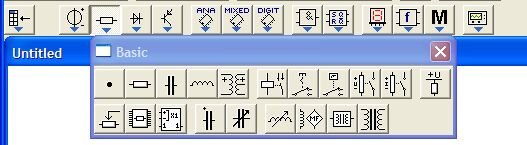
При нажатии на кнопку  откроется панель диодов, и пни нажатии на кнопку  откроется панель выбора транзисторов.
Для сборки электрической схемы следует перетащить (не отпуская левой кнопки мыши) нужные элементы на лист рисования электронных схем.
Постоянный электрический ток Закон Ома для участка цепи.
Соберём первую электрическую схему для исследования цепи постоянного тока. Для этого нам понадобится источник постоянного тока (напряжения) - battery  , электрическое сопротивление (резистор resistor) -  и измерительный прибор (амперметр, ammetr,) который находится на панели Indicators:
В итоге у нас получится такая картина:
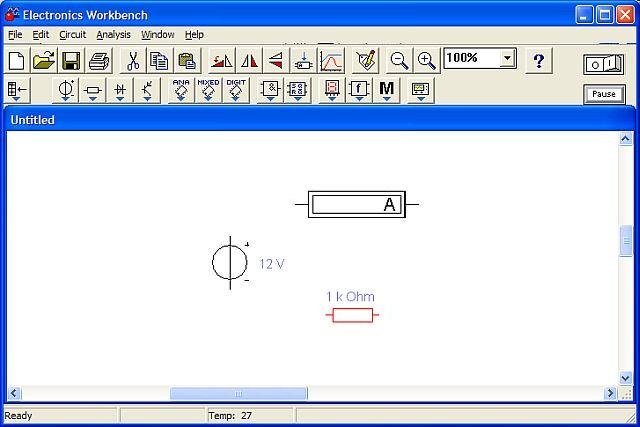
Для создания электрических соединений элементов схемы, следует подвести курсор мыши к контакту элемента (до появления чёрной точки на контакте. Рис. А) и, не отпуская кнопки мыши провести линию к контакту следующего элемента (до появления чёрной точки на контакте. Рис. Б) и отпустить кнопку мыши.
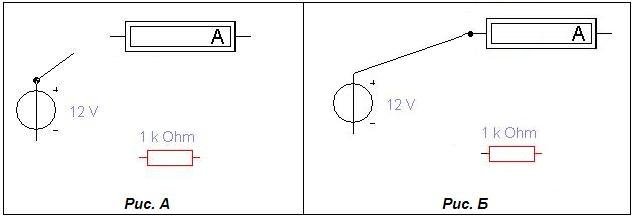
В итоге, должна получиться такая схема:
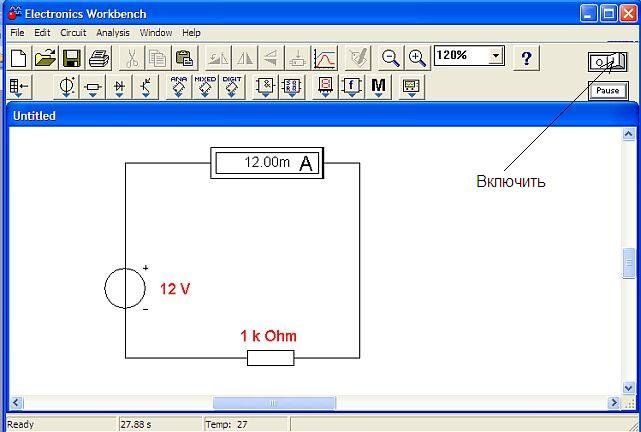
Далее следует включить включатель, показанный на рисунке. На амперметре отобразится величина электрического тока равная 12 мА (миллиампер).
Электрические величины, участвующие в наших экспериментах имеют следующие размерности:
Напряжение - вольты, в данном случае 12 V (вольт постоянного тока). При экспериментах, возможно, будут более низкие значения напряжения - милливольты (mV). 1 вольт = 1000 милливольт.
Ток - амперы, в данном случае доля ампера миллиампер (mA). 1 ампер = 1000 миллиампер.
Сопротивление - Ом. В нашем случае сопротивление имеет величину 1 Ком (kOhm). 1 килоом = 1000 Ом.
По закону Ома, между тремя величинами (ток - I, напряжение - U, сопротивление - R) существует математическая зависимость:
I = U/R, U = R*I, R = U/I
Используя формулы закона Ома, рассчитаем ток в нашей цепи:
I = 12/1000 = 0,012 А = 12 мА. Измеренный результат соответствует расчётному. Произведя измерение, следует выключить включатель  .
Попробуем изменить значения элементов схемы и, произведя расчеты сравнить результаты с измеренными. Изменим, например, значение сопротивления. Для изменения значений элементов схемы следует выделить элемент на схеме и нажать правую кнопку мыши. В появившемся локальном меню выбрать опцию "Component Properties".
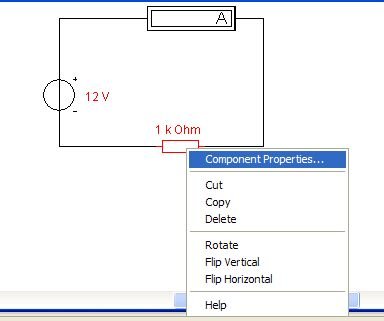
Далее, на панели "Resistor Properties", в закладке "Value", изменим значение "Resistance" на 100, а в поле множителя выберем Ом (омега).
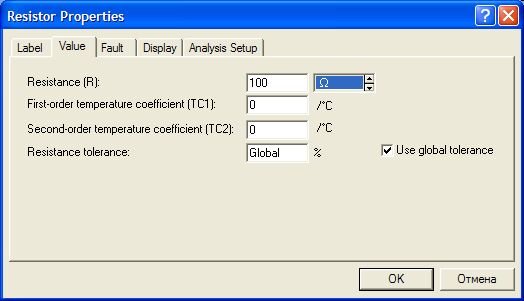
Заодно изменим значение напряжения источника питания с 12 вольт на 10 вольт:
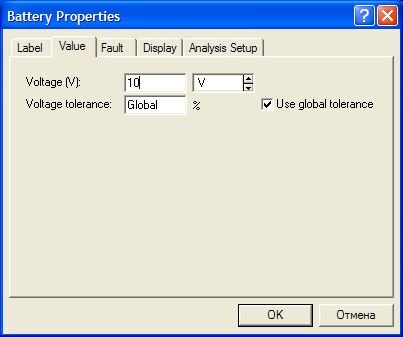
По закону Ома рассчитаем значение тока в новой цепи: I = U/R = 10/100 = 0,1 A = 100 mA. Включим питание и убедимся, что значения совпадают.
Последовательное и параллельное включение сопротивлений
Для следующего эксперимента соберём схему, показанную на рисунке.
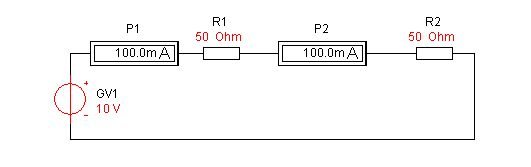
В цепи нашей схемы будет два резистора (R1 и R2) по 50 Ом включенные последовательно и источник питания (GV1) напряжением 10 вольт. При включении включателя схемы мы увидим, что ток, проходящий через последовательно включенные сопротивления одинаков в любой точке цепи - амперметры P1 и P2 показывают одинаковые результаты 100 мА. По закону Ома, рассчитаем общее сопротивление нашей цепи: R = U/I = 10/0,1 = 100 (Ом). Из схемы видно, что общее сопротивление цепи из последовательно включенных сопротивлений равно сумме этих сопротивлений (50 + 50 Ом).
Для включения обозначений элементов на схеме следует выделить элемент (например, сопротивление R1) и нажать правую кнопку мыши. В локальном меню выбрать опцию "Component Properties" и на панели "Resistor Properties" выбрать закладку "Label". В поле "Label" следует ввести нужное обозначение элемента - R1.
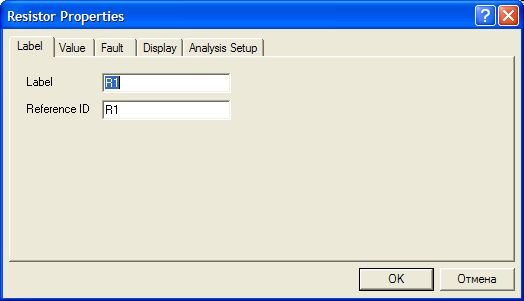
При параллельном включении сопротивлений, ток от источника питания будет разветвляться на сопротивления, и зависеть от их величины. Соберём схему, показанную на рисунке:
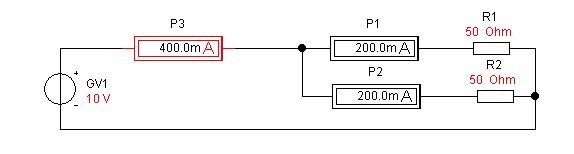
Из схемы видно, что общий ток (прибор Р3) равен 400 мА, а токи, проходящие через сопротивления, разделились и равны 200 мА. Сумма токов равна общему току. Так как величина сопротивлений R1 и R2 равна, то и токи равны. Изменим величину одного из сопротивлений, уменьшив его, например, до 10 Ом.
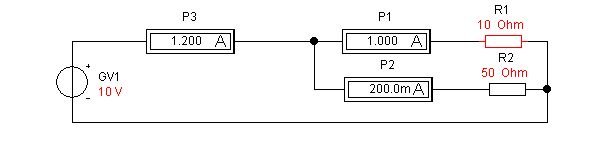
Мы видим, что с уменьшением сопротивления, ток в цепи этого сопротивления возрастает (Ir1 = 1А), а следовательно возрастает и общий ток Io = Ir1 + Ir2 = 1,2 А. Как рассчитать общее сопротивление цепи для параллельно включенных резисторов? Для этого воспользуемся формулой: 1/Ro = 1/R1 + 1/R2 = 1/10 + 1/50 = 0,1 + 0,02 = 0,12. В результате получим Ro = 1/0,12 = (8,33333333:) 8,3 Ом.
Общее сопротивление параллельно включенных сопротивлений всегда меньше меньшего из сопротивлений. В общем случае формула расчёта общего сопротивления из параллельно включенных n сопротивлений равна 1/Ro = 1/R1 + 1/R2 + ... + 1/Rn
Проверим правильность расчёта нашей цепи, найдя общий ток: I = U/R = 10/8,3 = 1,204819277108 = 1,2 A, что совпадает с показанием измерительного прибора Р3.
Делитель напряжения
Очень часто при проектировании электронных схем требуется получить напряжение несколько ниже напряжения источника питания. Для получения дополнительных напряжений служит резистивный делитель напряжения.
Соберём схему, показанную на рисунке:
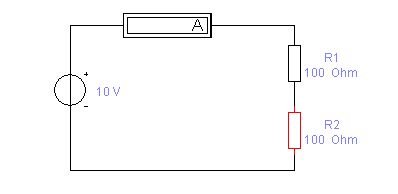
Для поворота элементов схемы служит кнопка "Rotate"  на панели системных кнопок.
По закону Ома рассчитаем ток, проходящий в цепи: I = U/R = 10/(R1 + R2) = 10/200 = 0,05 A (50 mA). Теперь рассчитаем напряжение на одном из резисторов, например R2.
Ur2 = I * R2 = 0,05 * 100 = 5V.
Мы видим, что напряжение на сопротивлении R2 равно 5 вольт. Для того чтобы убедиться в этом добавим на схему вольтметр и проведём измерения. По результатам эксперимента видно, что измеренные результаты совпадают с расчётными.
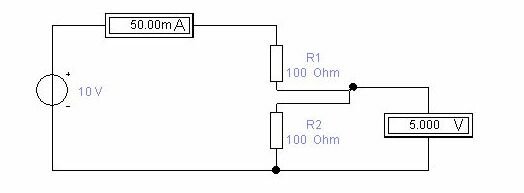
Изменим сопротивление резистора R2, например на 50 Ом и посмотрим изменения в показаниях приборов.
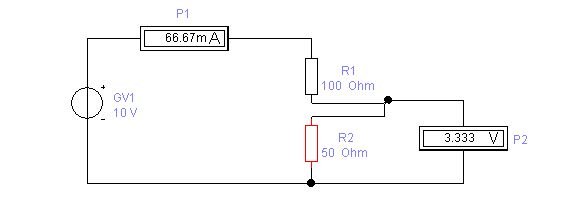
В реальных схемах принято резистор R1 называть гасящим сопротивлением, а резистор R2 - нагрузкой.
При получении пониженных напряжений следует учитывать ток нагрузки и напряжение источника питания, и, исходя из тока нагрузки, рассчитывать сопротивление гасящего резистора. Например, если мы используем в качестве нагрузки лампу накаливания на напряжение 3V и мощностью P = 2W(ватт), то нам следует сначала найти ток, проходящий через лампу:
I = P/U = 2/3 = 0.666666666667 = 0,67 А.
Зная ток через лампу, рассчитаем её сопротивление (сопротивление нагрузки):
Rн = U/I = 3V/0,67A = 4,477611940299 = 4,48 Ом.
И, наконец, зная ток в цепи и сопротивление нагрузки, рассчитаем сопротивление гасящего резистора R1 при напряжении источника питания Ugv1 равного 10 вольт:
R1 = Ugv1/I - Rн = 10/0,67 - 4,48 = 11 Ом.
Имея исходные данные, соберём схему и сравним измеренные величины (лампа находится на панели "Indicators"):
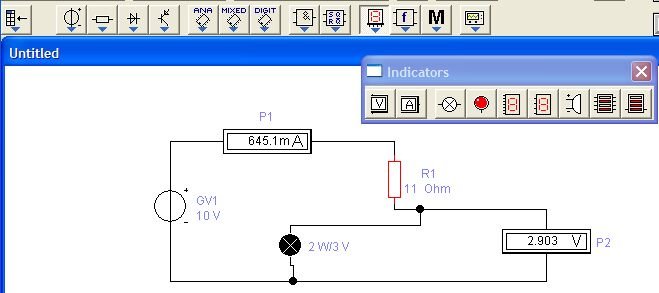
Мы видим, что рассчитанные нами величины близки к измеренным. При практическом изготовлении делителей напряжения следует учитывать мощность гасящего резистора. Рассчитаем мощность гасящего резистора для нашего случая. Мощность P рассчитывается по формуле:
P = R * I2 = 11 Ом * 0,67A * 0,67A = 4.9379 = 5 Вт. Мы видим, что мощность резистора должна быть не менее 5 Вт. Если использовать резистор с меньшей мощностью, то он будет перегреваться в процессе эксплуатации и перегорит.
Закон Кирхгофа
Следуя из закона Ома, закон Кирхгофа звучит так: сумма токов входящих в узел равна сумме токов выходящих из узла.
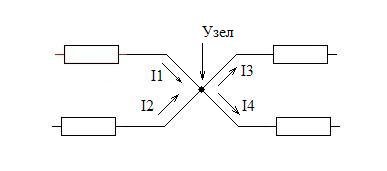
Например, на приведённой схеме, по закону Кирхгофа сумма токов I1 и I2 должна равняться сумме токов I3 и I4. Причём токов входящих в узел и токов выходящих из узла может быть сколь угодно.
Убедимся практически в справедливости закона. Соберём схему, показанную на рисунке:
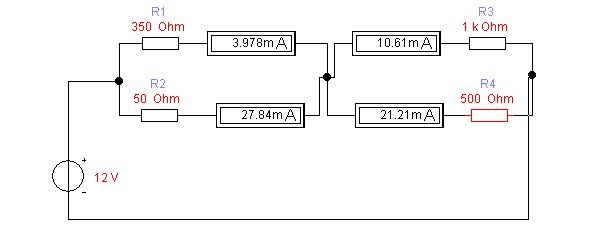
Введём абсолютно произвольные значения сопротивлений цепи и посмотрим токи, проходящие через эти сопротивления. Токи, проходящие через сопротивления R1 и R2 являются входящими в узел, а токи, проходящие через сопротивления R3 и R4 являются выходящими из узла. Проверим равенство
Ir1 + Ir2 = Ir3 + Ir4; 3,978 + 27,84 = 10,61 + 21,21; 31,818 = 31.82 - равенство подтверждается.
Закон Кирхгофа удобно использовать на участках электрических цепей, где некоторые токи неизвестны.
|
