
Простейший способ введения тригонометрических функций - с помощью прямоугольных треугольников.
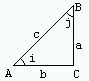
Отношение длины стороны BC (катета) к длине стороны AB (гипотенузы) называется синусом угла i, противолежащего катету BC:
Sin(i) = |BC| / |AB| или Sin(i) = a/c.
Отношение |AC| / |AB| называется косинусом угла i, прилежащего к катету AC:
Cos(i) = b/c. Отношение длин катетов |BC| к |AC| называется тангенсом, а обратное отношение называется котангенсом угла i:
Тангенс Tg(i)=a/b;
Котангенс Ctg(i)=b/a.
Из этих равенств следует, что:
Tg(i) = Sin(i) / Cos(i),
Ctg(i) = 1/Tg(i) = Cos(i)/Sin(i).
Очевидны формулы:
Sin(i) = Cos(j),
Tg(i) = Ctg(j).
Во всех приведенных формулах i и j - острые углы прямоугольного треугольника i, j < 90°
Важное замечание:
Радиан (rad) - это центральный угол опирающийся на дугу, длина которой равна радиусу окружности. В градусной мере 1 радиан равен примерно 57.29577951. Если значение g - в градусах, а r -в радианах, то g=r*180/pi. Где pi = 3.141592654. Прямой угол равен pi / 2 * rad; развернутый pi * rad; полный 2 * pi * rad.
Возьмем на плоскости луч OMo и будем поворачивать его вокруг точки О против часовой стрелки
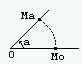
При повороте на угол а луч ОМо отобразится на луч ОМа; точка Мо пробежав часть окружности с центром в точке О, попадет в точку Ма. Если угол поворота прямой (а = pi/2), дуга МоМа - четверть окружности,
если угол поворота развернутый (a = pi) - полуокружность,
если угол поворота полный (a=2pi) - полная окружность, в этом случае Ма = Мо.
Рассмотрим круг единичного радиуса:
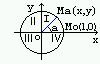
Круг имеющий центр в начале координат называется единичным кругом.
Точка Ма на его окружности получается из точки Мо (1,0) в результате поворота луча ОМо на угол а. Координаты точки Ма обозначим x и y, тогда очевидно, x^2+y^2=1 ( уравнение окружности).
Тригонометрические функции для произвольного угла определяются следующим образом:
Sin(a) = y,
Cos(a) = x,
Tg(a) = Sin(a) / Cos(a),
Ctg(a) = Cos(a) / Sin(a).
Формулы приведения предназначены для упрощения аргументов тригонометрических функций:
Sin(a + 2 * pi * n) = Sin(a), Cos(a + 2 * pi * n) = Cos(a),
Tg(a + pi * n) = Tg(a), Ctg(a + pi * n) = Ctg(a),
Sin(a + pi) = -Sin(a), Cos( a + pi) = -Cos(a),
Sin(a ±pi/2) = ±Cos(a), Cos(a ±pi/2) = ±Sin(a),
Tg(a ±pi/2) = -Ctg(a), Ctg(a ±pi/2) = -Tg(a).
В этих формулах n - любое целое число.
Свойство четности и нечетности:
Sin(-a) = -Sin(a), Cos(-a) = Cos(a),
Tg(-a) = -Tg(a), Ctg(-a) = -Ctg(a).
Функции дополнительных углов:
Sin(pi-a) = Sin(a), Cos(pi-a) = -Cos(a),
Sin(pi/2-a) = Cos(a), Cos(pi/2-a) = Sin(a).
Пример:
Sin(1873°) = Sin(73° + 360° * 5) = Sin(73°) = Sin(90° -17°) = Cos(17°).
Поскольку синус - немонотонная функция, то для введения обратной функции следует выбрать какой-либо промежуток монотонности синуса. Принято следующее определение.
Арксинус числа х (при х[-1,1]) - это угол y (y[-pi/2, pi/2]), синус которого равен х:
y=ArcSin(x), Sin(y)=x.
Арккосинус - обратная функция для косинуса:
y=ArcCos(x), Cos(y)=x; При x[-1,1], y[0,pi].
Арктангенс - обратная функция для тангенса:
y=ArcTg(x), Tg(y)=x; При x[-бесконечность,+бесконечность], y[-pi/2,pi/2].
Арккотангенс - обратная функция для котангенса:
y=ArcCtg(x), Ctg(y)=x; При x[-бесконечность,+бесконечность], y[0,pi].
Tg(a) * Ctg(a)=1,
Sin(a)2 + Cos(a)2 =1 (теорема Пифагора),
Sin(a ±b) = Sin(a) * Cos(b) ±Cos(a) * Sin(b),
Cos(a ±b) = Cos(a) * Cos(b) ±Sin(a) * Sin(b),
Sin(2*a) = 2*Sin(a) * Cos(a),
Cos(2*a) = Cos(a)2 -Sin(a)2,
Cos(2*a) =2 * Cos(a)2 - 1,
Cos(2*a) = 1 - 2 * Sin(a)2,
Sin(a) + Sin(b) = 2 * Sin((a+b)/2) * Cos((a-b)/2),
Sin(a) - Sin(b) = 2 * Sin((a-b)/2) * Cos((a+b)/2),
Cos(a) + Cos(b) = 2 * Cos((a+b)/2) * Cos((a-b)/2),
Cos(a) - Cos(b) = -2 * Sin((a+b)/2) * Sin((a-b)/2),
Sin(a) * Sin(b) = (Cos(a-b) - Cos(a+b)) / 2,
Cos(a) * Cos(b) = (Cos(a-b) + Cos(a+b)) / 2,
Sin(a) * Cos(b) = (Sin(a-b) + Sin(a+b)) / 2.