Прямоугольная система координат.
В математике (если не оговорено особо) применяется правая прямоугольная система координат.
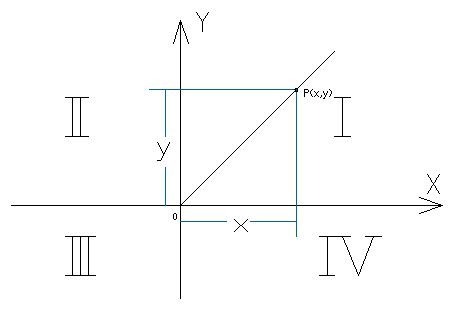 |
В правой декартовой прямоугольной системе координат направления осей выбираются так, что поворот оси 0x на угол 90 градусов в положительном направлении, т.е. в направлении противоположном вращению часовой стрелки, совмещает полуось положительных х с полуосью положительных y. Оси координат делят плоскость на четыре квадранта. Абсцисса х положительна для точек (x,y), расположенных в квадрантах I и IV, отрицательна в квадрантах II и III. Ордината y положительна для точек в квадрантах I,II, отрицательна для точек в квадрантах III, IV. |
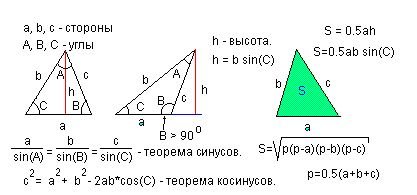
Уравнение прямой линии. Уравнение вида A*x+B*y+C=0, где А и B не равны нулю одновременно, определяют прямую линию. При С=0 прямая проходит через начало координат.
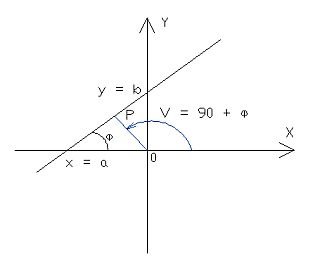
1)Уравнение прямой с угловым коэффициентом.
Прямая образующая угол ф (см. рис.) с положительным направлением оси 0х и пересекающая ось 0y в точке (0,b): y = k *x + b, где k = Tg(ф). Коэффициент k называется угловым коэффициентом прямой.
2)Уравнение прямой в отрезках.
Прямая линия пересекающая ось 0х в точке (a,0) и ось 0y в точке (0,b): x / a + y / b = 1; (a<>0, b<>0. <> - знак не равно).
3)Нормальное уравнение прямой.
Пусть р - длина перпендикуляра, опущенного из начала координат на прямую. Тогда уравнение прямой имеет вид:
x * Cos(v) + y * Sin(v) - p = 0.
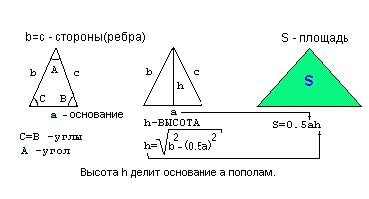
В прямоугольном треугольнике один из углов всегда равен 90 градусов (90°).
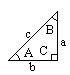
На рисунке это угол С(называется прямой угол). Сумма углов A и B также равна 90°, следовательно C = A + B.
По теореме Пифагора стороны прямоугольного треугольника (a,b,с) связаны следующей зависимостью a2 + b2 = c2. Две стороны (a,b) прилежащие прямому углу называются катетами, а сторона (c) противолежащая прямому углу называется гипотенузой.
Площадь прямоугольного треугольника: S = 0,5 * a * b.