
Пусть X - некоторое множество чисел. Если задано правило, которое каждому числу x принадлежащему X сопоставляет какое-нибудь число y, то такое правило называют функцией и записывают y = f(x).
При этом x называют значением аргумента (аргументом) функции f, y - значением функции в точке x.
Множество X чисел х, на котором задана функция f, называется областью определения функции (обозначается D(f)).
Множество чисел вида f(x), где x принадлежит D(f), называется областью значений функции (обозначается R(f)).
Способы задания функций:
1) Аналитический (формулой), например y = x2; y = Sin(x);
2) Графиком, например для функции y = k / x (при k>0):

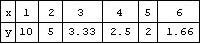
3) Таблицей, например для функции y = k / x при k =10:
Если y = f(x), то говорят, что переменные x и y связаны функциональной зависимостью; x называется независимой переменной, y - переменной.
1) Монотонность. Функция f(x) называется возрастающей на промежутке (a,b), если большим значениям аргумента соответствуют большие значения функции.
f(x2) > f(x1) при x2 > x1. Здесь предполагается, что промежуток (a,b) лежит в области определения функции и что x1,x2 - любые точки из (a,b).
Если выполняется f(x2) < f(x1) при x2 > x1 то функция называется убывающей на промежутке (a,b).
Возрастающие и убывающие функции называются строго монотонными. Неубывающие и невозрастающие функции - монотонными в широком смысле.
2) Периодичность. Функция f(x) называется периодической, если значения функции не меняются при изменении значений аргумента на некоторое постоянное число T <> 0: для любых х из области определения функции точки х ±T также принадлежат области определения и имеют место равенства: f(x+T) = f(x-T) = f(x). Число Т называется периодом функции. Если Т -период, то m * T - также период для любого целого m <> 0 (<> - знак не равно). Обычно под термином "период" подразумевают наименьший положительный период; например, Sin(x) и Cos(x) имеют наименьший период 2 * pi.
3) Чётность и нечётность. Функция f(x) называется четной, если для любых х из ее области определения выполняется равенство f(-x)=f(x). При этом предполагается, что область определения функции симметрична относительно точки х=0.
Функция f(x) называется нечетной, если f(-x) = -f(x).
4) Ограниченность. Функция f(x) называется ограниченной, если при всех х из ее области определения выполняется неравенство |f(x)| <= M или неравенство M1 <= f(x) <= M2, где M,M1,M2 - какие либо постоянные числа. Пример: |Sin(x)| <= 1.