
В случае когда, когда показатель степени n есть натуральное число, n -я степень произвольного действительного числа а (основания степени) есть произведение n множителей, равных а, то есть умножение числа а само на себя n раз. Записывается как an
Для степеней верны следующие равенства:
(ap) * (aq) = a(p+q);
(ap)q = a(p*q);
Далее, для любых действительных p и q (a>0, b>0):
a-p = 1 / ap;
ap / aq = a(p-q);
(a*b)p = (ap) * (bp);
(a / b)p = (ap) / (bp).
Арифметический корень n-й степени из числа (основания) а есть единственное положительное решение уравнения xn = a. Он обозначается a(1/n).
Если n = 2 то для вычисления корня (квадратного) существует запись
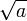 .
.Логарифм числа b при основании a можно определить как решение уравнения ax = b.
Обозначается: logab.
Выражения logab = x и ax = b равносильны.
Для логарифмов справедливы следующие равенства:
alogab = b;
logaa = 1; loga1 = 0;
loga(b*c) = logab + logac;
loga(b / c) = logab - logac;
На практике, особый интерес представляют десятичные логарифмы с основанием 10, (десятичные) обозначаются lg a, и логарифм с основанием 2,718282 (число е), натуральный, обозначается ln a.
Факториал n! произвольного целого числа n>=0 определяется формулами:
0! = 1;
n! = 1 * 2 * 3 * n-1 * n; например: 6! = 1 * 2 * 3 * 4 * 5 * 6 = 720.
Комплексные числа (иногда называемые мнимые числа) не являются числами в элементарном смысле слова, применяемыми при подсчетах и измерениях. Они составляют новый класс математических обьектов, определяемый описанными ниже свойствами:
Каждому комплексному числу z можно поставить в соответствие единственную пару (a,b) действительных чисел a и b и обратно. Комплексное число z = (a,b) состоит из действительной (вещественной) части a = Re(z) и мнимой части b = Im(z); Например: Re(3,-2) = 3, Im(3,-2) = -2.
Числа вида (а,0) отождествляется с действительными числами: (a,0)=a, поэтому понятие комплексного числа является расширением понятия действительного числа; в частности, число (0,0) совпадает с действительным числом 0. Числа вида (0,b) называются чисто мнимыми; в частности, число (0,1) называется мнимой единицей и обозначается буквой i (иногда j).
Правила действия с комплексными числами:
1) равенство (a1,b1) = (a2,b2) равносильно системе двух равенств a1 = a2, b1 = b2, т.е. два комплексных числа равны тогда, когда соответственно равны их действительные и мнимые части;
2) (a1,b1) + (a2,b2) = (a1+a2, b1+b2), т.е. при сложении комплексных чисел складываются отдельно их действительные и мнимые части; Например: (3,-1) + (-2,5) = (1,4);
3) (a1,b1) * (a2,b2) = (a1*a2-b1 * b2, a1*b2 + a2*b1); в частности i2= i*i = -1;
4) вычитание и деление определяются как операции, обратные соответственно сложению и умножению; деление на 0 не определено.
Комплексное число можно записать в так называемой алгебраической форме: z = a + ib;
Например: (-3,4) = -3 + 4i. Алгебраическая форма удобна тем, что все действия с комплексными числами выполняются как с двучленами (раскрытие скобок и т.д.), в которых после выполнения всех упрощений следует заменить i2 на -1.
Отсюда получается закон умножения комплексных чисел:
(a1 + i * b1) * (a2 + i * b2) = (a1 * a2 - b1 * b2) + i*(a1 * b2 + a2 * b1).
Примеры:
1) i3 = -i, i4= 1, i (n + 4) = in;
2) (-2 + 3i) * 4 + (1 + i) * (5 + 2i) = -8 + 12i + 5 + 5i + 2i + 2i2 = -5 + 19i.
Определение: если z = (a,b), то число (a,-b) называется комплексно сопряженным для z. Обозначим его zz. Тогда: z * zz = a2 + b/2 >= 0, Re(z) = (z + zz) / 2, Im(z) = (z - zz) / 2i.
Неравенства >, >=, <, <= между комплексными числами не определены.
Деление комплексных чисел удобно выполнять с помощью умножения делимого и делителя на число, сопряженное делителю. Например:
(2 + 3i) / (-1 + 2i) = ((2 + 3i) * (-1 - 2i)) / ((-1 + 2i) * (-1 - 2i)) = (-2 - 3i - 4i + 6) / (12 + 22) = (4 - 7i) / 5 = 0,8 - 1,4i.
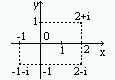
Комплексное число z = x + iy на плоскости отображается точкой с координатами (x,y).
Ось абсцисс (x) называется действительной осью, а ось ординат (y) - мнимой осью, плоскость называется комплексной плоскостью. Пара сопряженных чисел изображается точками, расположенными симметрично относительно действительной оси.
Комплексное число z=x+iy можно отождествить с вектором на плоскости xy, имеющим начало в точке 0 и проекции x и y.
Правила сложения и вычитания комплексных чисел совпадают с соответствующими правилами для векторов.
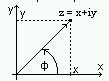
Модулем комплексного числа называется длина соответствующего вектора:
Abs(z) =
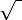 (x2 + y2) >= 0. Аргумент Arg(z) = ф - угол (в радианах) между вектором и положительной полуосью x. Для каждого z <> 0 существует множество значений ф, отличающихся одно от другого слагаемыми вида 2 * pi * k (k=0, +-1,+-2...).
(x2 + y2) >= 0. Аргумент Arg(z) = ф - угол (в радианах) между вектором и положительной полуосью x. Для каждого z <> 0 существует множество значений ф, отличающихся одно от другого слагаемыми вида 2 * pi * k (k=0, +-1,+-2...).Обычно используют главное значение аргумента: -pi < ф < pi (иногда 0 <= ф <2*pi).
Главное значение аргумента вычисляется по правилам:
1) (x>0, y>0) ф = ArcTg(y / x);
2) (x<0, y>0) ф=ArcTg(y / x) + pi;
3) (x<0, y<0) ф=ArcTg(y/x)-pi;
4) (x>0, y<0) ф=ArcTg(y / x).
Аргументы действительных и чисто мнимых чисел:
1) (x > 0, y = 0) ф = 0;
2) (x = 0, y > 0) ф = p i/ 2;
3) (x <0, y = 0) ф = pi;
4) (x = 0, y < 0) ф = -pi / 2.
Тригонометрическая форма комплексного числа:
z = p*(Cos(ф) + i * Sin(ф)), где p =
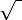 (x2 + y2).
(x2 + y2).Примеры:
1) 1 + 0*i = 1*(Cos(0) + i * Sin(0));
2) i = 1 * (Cos(pi / 2) + i * Sin(pi / 2);
3) 1 + i =
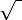 (2) * (Cos(pi / 4) + i * Sin(pi / 4));
(2) * (Cos(pi / 4) + i * Sin(pi / 4));4) 3 + 4 * i = 5(Cos(ф) + i * Sin(ф)).
Показательная форма комплексного числа:
z = Abs(z) * e (i*ф), или z = (p * e)(i*ф), где число е=2.7182818.
Например:
e(i*pi/2) = i;
e(2*i*pi*k) = 1.
Модуль(Abs) числа вида e(i*ф) равен 1 при любом действительном ф.