Математические функции.
Для математических вычислений в Turbo Pascal есть ряд математических функций. Наименования функций и методы их использования представлены в таблице:
|
Функция Pascal
|
Математическая функция
|
| sqr(x) |
Квадрат числа х |
| sqrt(x) |
Квадратный корень из числа х |
| abs(x) |
Модуль числа х |
| trunc(x) |
Целая часть числа х |
| frac(x) |
Дробная часть числа х |
| x div y |
Целочисленное деление x на y. Дробная часть числа отбрасывается. Например: 25 div 10 = 2 |
| x mod y |
Получение дробной части при делении х на y. Например: 25 mod 10 = 5 |
| exp(x) |
Число е (2,718282) в степени х |
| ln(x) |
Логарифм натуральный числа х |
| round(x) |
Округление числа х до ближайшего целого |
| inc(x,y) |
Инкремент - увеличение х на величину у. Если у не указано, то х увеличивается на 1 |
| dec(x,y) |
Декремент - уменьшение х на величину у. Если у не указано, то х уменьшается на 1 |
| randomize |
Включение генератора случайных чисел |
| random(a) |
Получение случайного числа в диапазоне от 0 до а (а - целое число) |
|
Тригонометрические функции (аргумент в радианах)
|
|
|
| sin(x) |
Синус аргумента х |
| cos(x) |
Косинус аргумента х |
| arcTan(X) |
Арктангенс аргумента х |
Для решения математических задач, в Паскале предусмотрены следующие математические операции: сложение (+); вычитание (-); умножение (*); деление (/); целочисленное деление (x div y); получение остатка от деления (x mod y). Для расстановки приоритетов в вычислениях расставляются круглые скобки.
Рассмотрим решение задачи на вычисление корней квадратного уравнения ax2 + bx + c = 0.
Для решения нам следует найти дискриминант уравнения D = B2 - 4 * A * C;
Если D = 0, корень один (двукратный): x = -(B / (2 * A));
Если D < 0, нет действительных корней
Если D > 0, имеются два действительных корня:
x1 = (-B + 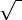 D) / (2 * A), D) / (2 * A),
x2 = (-B - 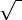 D) / (2 * A). D) / (2 * A).
Определим, какие переменные будут участвовать в решении уравнения.
Очевидно, что это аргументы a, b, c, дискриминант d и два корня x1 и x2. Так как переменные могут принимать любые значения, то выберем тип переменных real.
Программа решения квадратного уравнения будет выглядеть так:
uses crt;
var
a,b,c,d,x1,x2: real;
begin
{Вводим значения a, b и c}
clrscr;
write('Wwedite A: ');
readln(a);
write('Wwedite B: ');
readln(b);
write('Wwedite C: ');
readln(c);
{Вычисляем дискриминант}
d:= b*b - 4*a*c;
{Если дискриминант больше 0, то вычисляем корни и выводим на экран}
if d > 0 then
begin
x1:= (b - sqrt(d))/(2*a);
x2:= (-b - sqrt(d))/(2*a);
writeln('x1 = ',x1:0:4);
writeln('x2 = ',x2:0:4);
end;
{Если дискриминант равен 0, то вычисляем один корень и выводим на экран}
if d = 0 then
begin
x1:= -(b/(2*a));
writeln('Koren = ',x1:0:4);
end;
{Если дискриминант меньше 0, то выводим сообщение}
if d < 0 then
begin
writeln('Korney net');
end;
readln;
end.
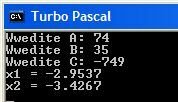
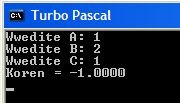
Результат решения уравнения при разных значениях дискриминанта:
  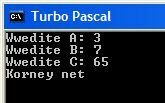
 Пользовательские процедуры и функции.
Пользовательские процедуры и функции.
При написании программ со сложными математическими вычислениями становится очевидным, что математических функций встроенных в Turbo Pascal, явно недостаточно. Нет, например такой функции, как y = xn. В процессе вычислений можно конечно задействовать такую формулу возведения в степень: y := exp(n*(ln(x)); но при частом использовании такой формулы в программе легко запутаться, особенно если нужно использовать разные аргументы.
Turbo Pascal предусматривает создание пользовательских процедур и функций. Рассмотрим создание функции возведения числа х в произвольную степень n (n >=0). Функция на паскале должна быть объявлена до начала программы, то есть до оператора begin.
Функция описывается следующим образом:
function имя функции (аргумент : тип аргумента) : возвращаемый тип данных;
var
раздел локальных переменных (если нужен);
begin
тело функции;
end;
В нашем случае с вычислением степеней, функция будет выглядеть так:
function stepen(x,n: real): real;
begin
stepen:= exp(n*ln(x)); {Результат возвращаемый функцией, присваивается самой функции}
end;
Теперь, напишем программу с использованием нашей функции.
uses crt;
function stepen(x,n: real): real;
begin
stepen:= exp(n*ln(x));
end;
var {раздел глобальных переменных}
rez,osn, pok: real;
begin
clrscr;
write('Wwedi osnowanie');
readln(osn);
write('Wwedi pokazatel');
readln(pok);
rez:= stepen(osn,pok);
writeln('rezultat= ',rez:0:2);
readln;
end.
Результат работы программы:
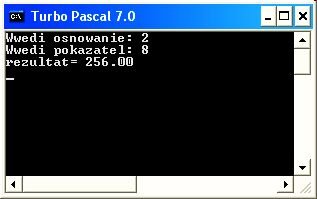
Используя уже написанные пользовательские функции можно создавать другие функции. Например, в нашем случае, мы можем написать функцию извлечения корня с произвольным показателем k (k <> 0) из любого числа q.
Известно, что q1/k = 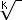 q Исходя из этих соображений напишем функцию извлечения корня: q Исходя из этих соображений напишем функцию извлечения корня:
function koren(q,k: real): real;
var
kr: real;
begin
kr:= 1 / k;
koren:= stepen(q,kr);
end;
Так как, функция koren, использует функцию stepen, то в тексте программы, функция koren должна быть описана после описания функции stepen. Дополним и изменим нашу программу, с учётом вычисления не степени, а корня:
uses crt;
function stepen(x,n: real): real;
begin
stepen:= exp(n*ln(x));
end;
function koren(q, k: real): real;
var
kr: real;
begin
kr:= 1 / k;
koren:= stepen(q,kr);
end;
var
rez,osn, pok: real;
begin
clrscr;
write('Wwedi osnowanie: ');
readln(osn);
write('Wwedi pokazatel: ');
readln(pok);
rez:= koren(osn,pok);
writeln('rezultat= ',rez:0:2);
readln;
end.
Извлечём, например, корень 8-й степени из 256:
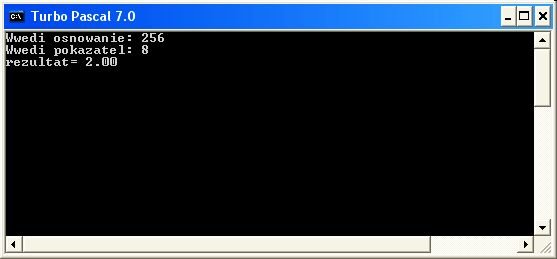
Процедуры в паскале, то-же, что и функции, но процедуры не возвращают никаких значений. Описываются процедуры так же, как и функции, в начале программы:
procedure имя процедуры (аргументы : типы аргументов);
var
{объявление локальных переменных, если нужно}
begin
{тело процедуры}
end;
Напишем процедуру, которая будет прекращать выполнение программы не по нажатию клавиши Enter (в нашем случае мы используем оператор readln в конце программы), а при нажатии любой клавиши:
procedure stop;
begin
repeat until keypressed; {в теле процедуры мы используем цикл, который прервётся только тогда, когда будет нажата любая клавиша на клавиатуре (о циклах подробно в следующих разделах}
end;
Для проверки работы процедуры, следует дописать её в начало нашей программы, а оператор readln; в конце программы заменить новым оператором - stop;

|

