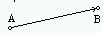
Пара точек A и B задает вектор AB, имеющий начало А и конец В. Будем векторы обозначать прописными буквами a...z. Вектор можно представить в виде направленного отрезка A,B
(рис.1).Модулем (абсолютной величиной) вектора AB называется длина отрезка AB и обозначается Abs(AB) или Abs(a). Так как вектор характеризуется не только длиной , но и направлением, то два вектора a и b будут равны если: Abs(a)=Abs(b) и их направления одинаковы.
Таким образом, например, вектору а соответствует бесконечное множество равных ему векторов, получаемых всевозможными параллельными переносами вектора а.
Действия с векторами:
1) Сумма а+b векторов a и b находится по правилу треугольника
или по правилу параллелограмма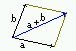 
Оба эти правила равносильны.
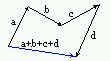
Правило треугольника удобно при сложении нескольких векторов
Разность векторов a-b можно определить как сумму a+(-b), т.е. вычитание заменяется прибавлением противоположного вектора. Удобно также правило треугольника: векторы a и b откладывают от общего начала, тогда разность a-b есть вектор, начало которого совпадает с концом b, а конец с концом а
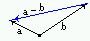
Произведением вектора а на действительное число m называется вектор, модуль которого равен Abs(a)*Abs(m), а направление при m>0 совпадает с направлением а, при m<0 противоположно направлению а. Таким образом умножение вектора на положительное число сводится к растяжению (сжатию при m равном правильной дроби) вектора, а умножение на отрицательное число - ещё и к изменению направления на противоположенное. Отметим, что 1 * a = a, 0 * a = 0.
Коллинеарные векторы - векторы, лежащие на одной прямой или на параллельных прямых.
Коллинеарные векторы отличаются лишь числовым множителем. Нулевой вектор (вектор начало и конец которого совподают - точка) колинеарен любому вектору.
Компланарные векторы - три или более векторов, лежащих в одной плоскости или в параллельных плоскостях. Любые три компланарных вектора вектора a,b,c связаны зависимостью: za + xb + yc = 0, где хотя бы один из коэффициентов отличен от 0.
Проекцией вектора на любую ось l называется произведение модуля вектора на косинус угла между вектором и положительной полуосью l: (a)=Abs(a)*Cos(ф). Ось l - это прямая, на которой выбрано положительное направление.
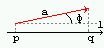
Очевидно, что (а) = ±Abs(pq), где p,q (прямая) - основания перпендикуляров, опущенных на ось из начала и конца вектора а. Знак ± означает: + острый угол, - тупой угол.
Координатами ax, ay, az вектора а в прямоугольной системе координат xyz в пространстве называются его проекции на координатные оси x,y,z:
ax = (a)x = Abs(a) * Cos(a),
ay = (a)y = Abs(a) * Cos(b),
az = (a)z = Abs(a) * Cos(y).
Здесь a,b,y - углы между и соответствующими полуосями.
При сложении векторов их соответствующие проекции складываются, при умножении вектора на число - умножаются на это число:
(a+b)x = ax + bx, (a+b)y = ay + by, (a+b)z = az + bz;
(m*a)x = m * ax, (m*a)y = m * ay, (m*a)z = m*az.
Модуль вектора a(ax,ay,az) вычисляется по формуле:
|a| =
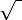(ax2 +ay2+az2).В случае векторов на плоскости xy справедливы те же формулы, но отсутствует третья координата; например:
|a| =
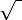(ax2 + ay2).Скалярное произведение a * b двух векторов a и b - это число, равное произведению модулей векторов на косинус угла между ними:
a * b = |a| * |b| * Cos(ab).
Скалярное произведение обозначается (ab), иногда (a,b). Если угол между векторами острый (тупой), скалярное произведение положительно (отрицательно). Скалярное произведение выражается через проекции векторов по формуле: a * b = ax * bx + ay * by + az * by.
Векторным произведением a*b двух векторов a и b называется вектор с, определяемый следующим образом:
1) |c| = |a| * |b| * Sin(ab), т.е. модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах;
2) c перпендикулярен a, c перпендикулярен b, т.е. вектор с перпендикулярен плоскости, в которой лежат сомножители;
3) векторы a,b,c образуют правую тройку векторов, т.е. кратчайший поворот вектора а к вектору b виден из конца вектора с как поворот против часовой стрелки
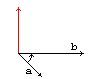
Если a и b колинеарны, то a * b = 0.
Свойства векторного произведения:
1) a * a = 0;
2) a * b = -b * a (векторное произведение антикоммутативно);
3) (a + b) * c = a * c + b * c;
4) (m * a) * b = m * (a * b).